Sinüzit Tedavisi için Basit Öneriler

Sinüslerin tıkanmasını önlemek ya da açmak için bir kaç adım atabilirsiniz.

Sinüzit hastalığı, salgı yoluyla üst solunum yollarını temizlemekle görevli olan sinüslerin iltihaplanması, tıkanması sonucu oluşuyor.

Sinüzit tedavi edilmez ise, hastalığın kronik hale gelmesi kaçınılmaz oluyor.

Amerika Birleşik Devletleri'nde Harward Üniversitesi Tıp Fakültesi tarafından internet üzerinden yayınlanan sağlık bülteninde, sinüslerin tıkanmasının önlenmesiyle sinüzit hastalığının tekrarlamasının önüne geçme şansı bulunduğu belirtiliyor.

Sinüzitin önüne geçmek, koronikleşmeden tedavisi ve tekrarının önlenmesi için antibiyotiklere başvurmadan önce sinüsleri açık tutmaya yönelik aşağıdaki basit öneriler sağlık veriliyor:

- Bol su için, kuruluk mukozanın sertleşmesine yol açar.

- Günde üç, dört kez buhar soluyun. Bir tencerede suyu ısıttıktan sonra, başınızın üzerinde bir havlu ile tencereye eğilip burnunuzdan derin nefes alın.

- Uyurken yastığınınızın yüksek olmasına dikkat edin.

- Alerjiye karşı alınan antihistamine türü ilaçlardan uzak durun, bu ilaçlar alejinize ve burun akıntısını durdurmaya iyi gelir ancak mukozayı sertleştirir.

- Burnunuza tuzlu su çekin, bu tür bir sprey kullanın.

- Yüzünüze ılık bir kompres yapmak sinüzitin yol açtığı ağrıyı hafifletir.Aspirin gibi ağrı kesiciler de yardımcı olur.

- Nazal dekonjestan kullanabilirsiniz ancak, tansiyon ve nabız yükselmesi gibi yan etkileri olabileceğini unutmayın.

- Son öneri ise, iki üç gün içinde sıkıntıların sürmesi durumunda doktorunuza danışarak önereceği antibiyotiğe başlamak.

Suyun Rengi Yok Mu?

Suyun dünyada bütün canlıların yaşam kaynağıdır. Vücudumuzun ve dünyanın büyük bir kısmı sıvıdır.Su özünde hidrojen ve oksijenin birleşiminden oluşmuştur ancak içtiğimizin suyun içerisinde çok fazla mineraller bulunmaktadır.Bu kadar etkenden sonra suyun renginin ne olmasını beklersiniz…

Alışıldık cevap suyun rengi olmadığıdır; su “şeffaf” ya da “saydam”dır ve denizin mavi görünmesinin tek sebebi gökyüzünün denizin üzerine yansımasıdır. Ancak bu doğru değil. Su aslında son derece soluk bir tonda olsa da mavidir. Bunu doğada, kardaki derin bir deliğe ya da donmuş bir şelalenin kalın buzlarının içine baktığınızda görebilirsiniz. Çok büyük ve çok derin beyaz bir havuzu suyla doldurup içine baktığınızda, su mavi görünecektir.

İnternetten Alışveriş Hakkında Merak Ettikleriniz !

Son günlerde bu sorular oldukça sık sorulmaya başlandı.Herkesin aklında kredi kartı bilgilerini internet sitelerine verip vermemekte kuşkular var.Bu kuşkuları ortadan kaldıracak bir topic yapalım herkes memnun kaldığı siteleri veya sorun yaşadığı siteleri nedenleriyle belirtirse güzel hepimiz için güzel bir rehber oluşturabiliriz. 

İnternetten alışveriş yapmadan önce 

1-) Alışveriş yapacağınız sanal mağazanın telefonunu, adresini, elektronik posta adresini, ve adını tam olarak açık ve net bir şekilde veriyor mu?Eğer o mağaza güvenilirse bu bilgileri çok açık ve net bir şekilde vermesi lazım.Aksi takdirde bir problem halinde kimin ile irtibat kuracağınız çok önemlidir. 

2-) Satın almak istediğiniz ürün hakkında, mağaza tarafından detaylı bir açıklama sunulmuş mu?Aksi taktirde, size gelen ürün, eğer istediğiniz ürün değilse, bunun için bir ispata ihtiyacınız vardır ve o açıklamanı bir kopyasını sizde kendinize alırsanız, ispat etmeniz hiç de zor olmayacaktır.

3-) Mağaza tarafından satın alacağınız ürünün fiyatı ve ek ücretler, vergiler vb. şeyler ne kadar miktar tutmuş?Net olarak bildirilmiş mi? 

Kesinlikle cevaplanması gerek sorular : 
+Ürünün toplam fiyatı 
+Teslimat şartları 
+Ödeme Koşulları 
+İptal ve iade halindeki durumlar 

4-) Ürünü satın aldıktan sonra size kaç günde ulaşacağı belirtilmiş miverwirrt en geç süreyi vermeleri lazım) 

5-) Artık ürününüzü seçtiniz ve kredi kartı şifrenizi ve bilgilerinizi vereceksiniz.Kredi kartı şifresini vereceğiniz sayfanın adres çubuğunda HTTPS:// olması gerekir. 

6-) Eğer yabancı bir firmadan alışveriş yapıyorsanız, dikkat etmeniz gereken bir şey vardır ki, herhangi bir mağduriyet halinde, sizin ülkenizin kanunları geçerli olmayacaktır.Ayrıca oradaki mağazanın müşteri hizmetlerini aradığınızda yabancı bir görevliyle saatlerce konuşabilme ihtimalini de göz önüne alırsak, kesinlik tanınmış şirketlerden alışveriş yapmalıyız. 

7-) Alışveriş yaptığınız mağazada gizlilik sözleşmesi diye bir bölüm olmalı!Aksi takdirde sizin tarafınızdan verilen bilgiler başka amaçlar içinde kullanılabilir.Elektronik Postanıza reklam amaçlı postalar gelebilir. 

8-)Kredi kartı bilgilerinizi verirken güvenlik paketi ile korunmakta olup olmadığına dikkat ediniz (global sign gibi) 

http://www.uzmantv.com/...e-mutlaka-dikkat-edelim 





İnternette alışveriş yapmak güvenli mi ? 

Internette alışveriş yaparken ,telefonla alışverişteki aynı sorunları yaşayabilirsiniz. 
Siparişimi alan kimse gerçekten yetkili bir kişi mi(dolandırıcı mı degil mi) 
Birileri ben siparişimi verirken telefon hattını dinleyerek benim kredi kartı numaramı çalabilir mi ? 

Gerçek hayatta kredi kartınızı kasiyerlere ,garsonlara (istemeyerek de olsa karınıza:) veya telefon üzerinden yetkili farzettiğimiz kişilere rahatlıkla veriyorsunuz. Aslında internette alışveriş yaparken kredi kartınızı kullanmanız gerçek hayattakinden daha tehlikeli değil. Hatta internet üzerinden alışveriş gerçek hayattakinden daha güvenlidir denilebilir çünkü alışverişi gerçekleştiren firma sizin internet tarayıcınızı kullanarak yapmakta olduğunuz alışverişi şifrelerler. Böylelikle alışveriş bilgileri siz ve alışveriş yaptığınız firma dışında üçüncü bir şahıs ya da kurumun eline geçerse okunması mümkün olmayacaktır. 

Netscape ürünleri bu güvenlik tehtitlerini SSL denen bir teknolojiyle önlemeye çalışırlar. SSL internete bağlı olan bilgisayarlar tarafından uygulanan bir dizi kuraldır. 

Bu kurallar sizin verilerinizin bütünlüğünün korunmasını iletim sırasında verilerin değistirilmemesini ve başka birilerinin eline geçmemesini ve verilerin ulaşması gereken karşı tarafın gerçekten yetkili kişi olmasını sağlar. 

Bir sitenin güvenli olup olmadığını anlamak için tarayıcınız üzerinde yazdığınız sitenin adresine bakın. Http adresinin sonuna eklenen “s” harfi yani “https” bağlandığınız site SSL protokolunun çalıştığını gösterir. Netscape 3.0 ve daha aşağı sürümlerde ekranın sol alt köşesinde kırık anahtar sembolü gözükür. Netscape 4.0 ve 4.5 ‘te kırma kilit sembolü güvenli modda kaybolur. Internet Explorer ‘da ise kapalı bir kırma kilit gözükür. 

Eğer SSL kullanmayan bir siteye bilgi göndermek üzereyseniz tarayıcınız sizi uyaracaktır. 

SSL , verilerinizin transferi sırasında güvenlik sağlamaktadır. Ancak siz kendinizi güvenilir sitelerden alışveriş yaparak koruyabilirsiniz.Bu sitelerin de sizin kredi kartı bilgileriniz başkalarıyla paylaşmayacak bir site olmasına dikkat ediniz. 

Not: alıntıdır... (Olympus Security)

Federal Ticaret Kurumu kredi kartı yolsuzluğu ve internet üzerindeki diğer sahtekarlıklarla mücadelesini sürdürmektedir. Bu konuda karşılaştığınız sorunları bildirmeniz için bir izleme komitesi kurulmuştur. http://www.fraud.org/ifw.htm

Güvenlik yönüne değinirsekte en güvenilir sitelerin bir arada bulunduğu kampanyadunyam.netlioo.com sitesine uğramanızı kesinlikle  tavsiye ederim.Onlarca firmanın indirim kuponlarınında bulunduğu bu site sayesinde alışveriş yaparken cebinizide düşünmüş oluyorsunuz. Eğer siteyi yararlı bulursanız üye olmanızıda tavsiye ediyorum üyelik linki: https://netlioo.com/register/
Merak ettiğiniz diğer bilgiler için yorumlarınızı bekliyorum.

Hemoroid Hastalığında Beslenme

Hemoroidde ne yemeli ne yenmemeli ?

Hemoroid hastalığında genetik yatkınlıktan (ailesel yatkınlık) sıkça söz edilmektedir,aslında burada kişnin vücudunda yatkınlıkmı olduğu yoksa o ailenin beslenme alışkanlaıklarınınmı sebep açık değilidir.Bazı ailelerde beslenme ve buna bağlı olarak dışkılama (kabızlık olması) alışkanlığı hemoroidde en önemli etkidir,benzer şekilde tuvalette 30-50 dakika kalmak gibi kötü tuvalet alışkanlığıda bazı ailelerde sık rastlanan bir durumdur ve buda beslenmeyle ilişkili olabilir.Acı tüketimide bazı toplumlarda daha yaygındır,acının direk etkisi olmasada makattaki yanma hissi ıkınmaya sebep olarak hemoroid riskini artırmaktadır.

   Bütün bunlar birlikte düşünüldüğünde hemoroid sebepleri arasında en önemli etkinin beslenme alışkanlığı olduğu söylenebilir.

Hemoroid hastalığı oluşumunu engellemek,hemoroidin ilerlemesini durdurmak ve hemoroidden kaynaklanan şikayetleri azaltmak için beslenmede şunlara dikkat edilmeli;

Hemoroide hastalığında tüketilmesi önerilen gıdalar:

-Kepekli ekmek;daha doğaldır ve barsakta posa bıraktığı için kabızlığı engelleyerek faydalı olur her zaman beyaz ekmeğe tercih edilmeli.

-Sebze :Her yemekte olabildiğindce fazla tüketilmelidir barsakta posa bıraktığı için barsağın rahat çalışmasını sağlar ve kabızlığı engeller.

-Meyve :imkanlar dahilinde her akşam meyve tüketilmeye çalışılmalıdır,sebze gibi barsakta posa bıraktığı için barsağın rahat çalışmasını sağlar ve kabızlığı engeller.

-Kayısı : Kabızlık tedavisinde kayısının ayrı bir yeri vardır,diğer meyvelerden farklı olarak kayısı barsak hareketlerini artırarak kabızlığı çözer.kayısı taze,kuru,komposto veya kayısı suyu olarak tüketilebilir ve hepsi etkilidir.

Tüm bunlara rağmen kabızlık problemi çözülemiyorsa her akşam 1-2 su bardağı kepek, çorba veya ayran ile karıştırılarak yenilebilir.



Hemoroid hastalığında tüketilmemesi gereken gıdalar:

Aslında bazı gıdalar suçlanarak yasaklansada bu yasakları genellemeden kişiye özel hale getirmek daha doğru olacaktır.

-Acı gıdalar;Acı yemek hemoroid sebebi değildir ama acı yenildiğinde yanma hissiyle tuvalette fazla ve şiddetli ıkınmak yada tuvalette uzun kalmak hemoroide sebep olabilir,hemoroidden kaynaklanan şikayetleri artırabilir.Eğer acı yediğinizde tuvalette fazla ıkınmıyorsanız acı yemenin zararı yoktur hatta dılkıda yumuşama yaptığı için fayda bile sağlayabilir.

-Kabızlığa sebep olan gıdalar;kişide kabızlığa sebep olan gıdalar tüketilmemelidir örneğin muz bir çok kişide kabızlık yapabilmektedir.

-Makat bölgesinde tahrişe sebep olabilen gıdalar;bazı hastalarda domates,patlıcan ve baharatlar şikayete sebep olmaktadır bu durumda kişi o gıdaları seçip onlardan uzak durmalıdır.

PİRİNÇ TÜKETMEK İÇİN 10 NEDEN..

NEDEN PİRİNÇ TÜKETMELİYİZ? 

Ülkemizde 30 yıl öncesinde kişi başı yıllık 4-5 kilogram tüketilen beyaz pirincin, günümüzde kişi başına yıllık 9-10 kilogramlar kadar tüketildiğini belirten Diyetisyen Selma Önelge Gür, beyaz pirincin faydalarını anlattı. “Pirinç içerdiği vitaminler bakımından oldukça değerlidir. Yüzde 80 karbonhidrat, yüzde 7 protein, yüzde 2 yağ, 10 mg kalsiyum, 0,9 mg demir, 0,08 mg B1 vitamini (Tiamin), 1,6 mg Niasin, 94 mg fosfor, 92 mg potasyum, 0.3 gr posa içerir. Kolesterol içermez. Kabuğu tam olarak ayrılmamış pirincin besin değeri daha yüksek ve posa oranı daha fazladır. Pişirirken besin kaybını önlemek için fazla yıkamamalı, kaynar su veya tuzlu suda ıslatmamalı ve yağda kavurmamalıdır. Bunun yanında tüketirken şunlara dikkat etmek gerekir:
• Pirinç satın alırken, kirli olmamasına, yabancı cisimler içermemesine ve nemlenmiş olmamasına dikkat edilmelidir.
• Serin ve kuru ortamda, kuru erzak kilerinde depolanmalıdır. • Kullanmadan önce ılık suyla yıkanmalıdır.
• Zengin nişasta içeriği bakımından birçok bakteri ve küf açısından iyi bir besi yeridir. Özellikle hasat sonrası uygun saklanarak, 1 yıl içerisinde tüketilmelidir.
• Piştikten sonra kısa süre içinde tüketilmeli, uzun süre bekleyen pişmiş pirinç besin zehirlenmelerine neden olabilecek riskli bir besindir.

Neden Pirinç Tüketmeliyiz? İşte, 10 Neden…

1. Karbonhidratların iyi bir kaynağıdır. Günlük enerjimizin yüzde 50’sinin karbonhidratlardan alınması söz konusudur. 100 gr pirinç 360 kalori verir. Glisemik indeksi sofra şekerine göre daha düşüktür. Sebze ve salatalarla birlikte tüketildiğinde kan şekerini hızla yükseltmez. Pişmiş iki yemek kaşığı pirinç ortalama 1 dilim ekmeğe eşdeğerdir.
2. Alerjen öğeler içermez. 6. ayını dolduran bebeklerde muhallebi yapımında pirinç unu kullanılması önerilir.
3. Bitkisel besinler içerisinde iyi dereceli protein kaynağıdır. Yoğurt, yumurta, baklagillerin yer aldığı menülerde pirinçten gelen protein değeri daha da artar.
4. Gluten içermez. Bu nedenle çölyak hastaları rahatlıkla kullanabilir.
5. Kabuksuz pirincin lif içeriği çok az olduğundan ishal tedavisinde yaygın olarak kullanılır.
6. Sporcuların artan karbonhidrat gereksinimi için iyi bir kaynaktır. Sporcuların fazla proteine değil karbonhidrata gereksinimleri vardır. En ekonomik yakıt karbonhidratlardır.
7. Tek başına şişmanlatmaz. Aslında hiçbir yiyecek tek başına şişmanlatmaz. Yeter ki kişi ihtiyacı olan enerjiyi yeterince alsın ve harcasın. Harcanmayan fazla enerji kaynağı ne olursa olsun şişmanlığa neden olur.
8. İçerdiği bol potasyum ve az azot ile kan basıncı değerlerinin düzenli akışını sağlar. Bu özelliğinden dolayı hipertansiyon ve böbrek hastalarında sık tüketilmesi uygundur.
9. Pirinç B gurubu özellikle B1 ve B2 vitaminlerince zengindir. B grubu vitaminler enerji oluşumunda yardımcıdır. Karbonhidrat, protein ve yağların vücutta kullanımı için gerekli yardımcı enzimlerin aktivitelerinde etkindirler.
10. Besleyici ve hazmı kolay olduğundan hastaların başlıca yemeğidir.

Matematiği İlk Kim Bulmuştur?

Tarihte matematiksel düşünce ölçme, borç, vergi, astronomi hesapları gibi pratik problemlere çözüm tekniklerinin geliştirilmesiyle başladı. Eski Yunan’da başlayan felsefeyle etkileşimi, matematiği genelleme ve soyutlamalara qürdü.Öte yandan bu genelleme ve soyutlamalar matematiğin kullanım alanını genişletti. Matematik’te genelleme ve soyutlamalara çok rastlanır .Birbirinden farklı görünen çok sayıda probleme tek bir prob-lemin özel durumları olarak bakılabilir . Örneğin üçgenlerin alanlarını tek tek hesaplamaya çalışmaktansa problemi genelleyip üçgenin alan formülünü türet-mek hem daha kolaydır,hem de böylece daha geniş bir uygulama alanı ortaya çıkar.

Günümüzde matematik kendi dinamiğinin yanı sıra başka bilimlerle arasındaki etkileşim nedeniyle de çok hızlı bir gelişme göstermektedir. Bu gelişmenin sonucu matematik içinde çok sayıda dal ortaya çıkmıştır (Analiz,aritmetik;cebir;geometri;istatistik;kümeler kuramı;olasılık kuramı; sayı-sal çözümleme;trigonometri). İlkel dinler incelendiğinde sayma gibi basit görünen bir işlemin oluşmasında toplumlar ancak ilk birkaç sayıya isim koya-bilmişler,gerisini “çok “olarak nitelemişlerdir.Matematiksel düşüncenin ilk adı-mı olan rakamlar ve sayma işlemi ancak ekonomisi düzenli,gelişmiş yerleşik toplumlarda yazı ile birlikte ortaya çıkmıştır.

Antik Çağda ilk önemli matematik merkezi olarak ,İÖ 2000’lerden sonra Babil görülür.Babilliler ekonomik yapılarının gerektiği denklem çözme,kök bulma,alan ve hacim hesaplama gibi tekniklerin yanı sıra astronomiye olan yakın ilgileri nedeniyle Trigonometriyi geliştirdiler.Babil’in matematiğe belki en büyük katkısı 60 tabanlı sayı sistemidir.Sıfır simgesinin de katılmasıyla onlu sisteme çok benzeyen 60 tabanlı sayı sistemi bugün bile açı ve zaman ölçümünde kullanılmaktadır.

Eski Mısır’dan günümüze ulaşan iki önemli matematik yapıtı Golenişev papirüsü(İÖ y.1900) ile Rhind papirüsüdür ( İÖ 1700’den önce).Bunlar çağlarının aritmetik ders kitapları olarak nitelenebilir.Gerek Mısır’da gerekse daha sonra Roma uygarlığında matematik,pratik bir araç olmaktan öteye gitmemiştir.Yunan matematiği İÖ 7-6. yüzyıllarda Mezopotamya ve Mısır’dan gelen bilgilerin derlenmesiyle oluştu,ama kendi ürünlerini İÖ 5. yüzyılın ikinci yarısından sonra vermeye başladı.Elealı Zenon’un zaman ve uzayın sonsuz sayıda parçaya bölünmesi hakkındaki paradoksları,Demokritos’un atomcu görüşleri,geometrik niceliklerin ölçümünde rasyonel sayıların (tamsayıların birbirlerine oranları)yeterli olmadığını buldular ve irrasyonel sayıların geometrik kuramını geliştirdiler.Alan ve hacim hesaplarındaki sonsuz küçük kesitler bugünkü integral kavramının ilk işaretleri olarak görülebilir.
Kuramsal matematiğin sonsuz kavramı dışında Eski Yunan matematiğin ilgilendiği iki önemli konu konikler ile astronomiden kaynaklanan küresel geometri problemleri oldu.İÖ 4. yüzyılın sonunda matematikte erişilen düzey ve yetkinlik daha sonra yazılan Eukleides’in ünlü Stoikheia’sı (Elemanlar)ile simgeler.

Kuramsal matematik Antik Çağda Arkhimedes ve Apollonios ile doruğa ulaştı.Konikler konusunda erişilen bulguların önemi ancak 19.yüzyılda izdüşümsel geometrinin gelişmesiyle anlaşılabildi.Arkhimedes ve Apollonios’tan sonra gelişme astronomiden kaynaklanan problemler doğrultusunda oldu. Gezegenlerin yörüngelerinin belirlenmesi ,sayısal tablolar,mekanik aygıtların bulunması ve İS 100 dolaylarında Melenos’un küresel trigonometrideki sonuçları Ptolemaios’un İS 2. yüzyılda astronomide ortaya koyduğu bulgulara temel oluşturdu.İS 4. Yüzyıldan sonra bilim eski bulguların yeniden gözden geçirilmesi ve öğretilmesine dönüştü.Klasikler yeniden yorumlandı,eski kitaplar üzerine yeni tezler yazıldı.Zaman içinde bu hep böyle süregidince Bizans dönemine Yunan matematiğinin yalnızca basit bir özeti kaldı.

Ortaçağda bilim Hindistan’da ve İslam dünyasında yeniden canlandı.Bağdat’ta Abbasi halifesi Mansur’un etkisiyle Yunan bilim yapıtlarının sistematik bir biçimde çevrilmesine girişildi.Hint astronomisinin de etkisiyle Bağdat ilk İslam astronomi merkezi oldu.Matematik ve astronominin bu yeniden canlanışında önemli etkenlerden biri de Bağdat okulundan Harizmi(y. 780-y. 850)oldu.Bu canlanış özellikle trigonometri ve küresel trigonometride Antik Çağdakinin çok üstünde bir gelişme doğurdu.İslam matematik ve astronomi geleneği 1400’lere değin aralıksız sürdü.

İslam biliminin Avrupa’ya yayılması 11. yüzyılda başlar.Bu konuda öncülüğü yapanlar 11. yüzyılda ;İngiliz filozof Bath’lı Adelard ve 12. yüzyılda İtalyan matematikçi Leonardo Pisano’dur.Bu yüzyıllarda Yunan bilim klasikleri Arapça çevirilerinden bu kez Latinceye çevrildi.Bu yapıtlar Rönesans’ın bilim yönünden temelini oluşturdu.

16. yüzyılın ortalarında Kopernik’in astronomi,Vesalius’un anatomi alanındaki bulguları eski klasiklerin yanlışlarını ortaya çıkarmıştı.Matematikte yeni bir çağı müjdeleyen ilk bulgular İtalya’da del Ferro, Cardano,Tartaglia ve Ferrari’nin üçüncü ve dördüncü derece denklemlere çözüm getirmeleri oldu.16. yüzyılın sonlarında Fransa’da Viéte’nin bilinmeyen büyüklükler için harflerle işlem yapması çok hızlı gelişecek olan simgesel cebirin temelini attı.

17. yüzyılda İskoçya’da Napier logaritmayı buldu.Cavalieri,Kepler’in sonsuz küçüklerle ilgili yöntemlerini geliştirerek geometriye uyarladı.Örneğin,elipsin bu yöntemle hesaplanabildi.1637’de Fransız filozof-matematikçi Descartes büyük buluşu analitik geometriyi ortaya koydu.Fermat’nın da katkılarıyla analitik geometri,geometri problemlerini cebirsel problemlere dönüştüren yeni bir araç oldu. Matematiği bir yan uğraş olarak sürdüren Fermat’nın sayılar kuramındaki bulguları ve Pascal’la birlikte kurduğu olasılık kuramı ona en büyük amatör matematikçi unvanını kazandırmıştır.

Newton ve Leibniz’in 17. yüzyılın ikinci yarısında diferansiyel ve integral hesabı bulmaları matematikte çok önemli bir adımı simgeler.Newton’un Philosophiae naturalis principia mathematica (1687;Doğa Felsefesinin Matematik İlkeleri)adlı yapıtı da gelmiş geçmiş en büyük bilimsel yapıt olarak kabul edilir.B u yapıtında kütleçekimi yasasını da ortaya koymuş olan Newton’un temel amacı doğayı anlamaktı; buna karşılık Leibniz bilgiye ve evrensel niteliklere ulaşan yolu açmak istiyordu.Leibniz’in bu amaçla geliştirmeyi tasarladığı simgesel mantık,George Boole tarafından ancak 19.yüzyılın ortalarında ortaya konabildi.Ama onun diferansiyel yöntemi 18. Ve 19. Yüzyıl matematiğinin gelişmesine temel oluşturdu.

18.yüzyıl matematiğinin en önemli adı Leonhard Euler’dir.Değişimler hesabı ve diferansiyel geometrinin kurucuları arasında yer alan Euler,analiz ve sayılar kuramı başta olmak üzere matematiğin hemen her dalına önemli katkılarda bulunmuştur.18. yüzyılın öteki büyük matematikçileri arasında J.-L.Lagrange,J.L.R.d’Alembert,P.-S.Laplace ve G.Monge anılabilir.

19.yüzyılda önemli bir gelişme Eukleidesçi olmayan geometrilerin ortaya konmasıdır.Eukleidesçi geometri (*)Stoikheia’da belirlenmiş olan beş aksiyom üzerine kurulmuştu.Bir noktadan ,verilen bir doğruya yalnızca bir paralel çizilebileceğini belirleyen beşinci aksiyomu,matematikçiler,yüzyıllar boyunca öteki aksiyomlara dayanarak kanıtlamaya çalışmışlar,ama bunda başarılı olamamışlardı.19. yüzyılın en büyük matematikçilerinden biri de, matematiğin hemen her dalına önemli katkılarda bulunmuş olan C.F. Gauss’tur.20. yüzyılın matematiğinde etkin bir yol gösterici de Hilbert ‘in 1900’de Paris’te İkinci Uluslararası Matematik Kongresi’nde önerdiği 23 problem olmuştur. Güncel birçok soru ve araştırma alanı, kaynağını Hilbert’in bu problemlerinden almaktadır.

TÜRK – İSLAM BİLGİNLERİNDEN EBU REYHAN MUHAMMED BİN AHMED EL-BİRUNİ’NİN HAYATI

(973-1048 ya da 1051/52).Büyük İslam bilgini Ebu Reyhan Muhammed Bin Ahmed el- Biruni,Batı Harzem’in başkenti Kas’ta (Ket) doğdu.Biruni’nin yaşamı üstüne yeterli bilgi yoktur.Kendi yazdıklarından,babasını küçük yaşta yi-tirdiğini,annesinin onu odun toplayıp,satarak büyüttüğünü öğreniyoruz.Harezm-şahlar soyundan ünlü bir bilginin koruyuculuğu altında saraya giren Biruni as-tronomi ve matematik öğrenimi gördü.Harezm sarayında çıkan kargaşalıklar sırasında bir süre İran’da kaldı,daha sonra da Sultan Kâbus bin Vaşmgir’in sara-yına kabul edildi.Bu kargaşa döneminde,henüz 28 yaşındayken önemli bir yapıt olan “El-Âsâru’l-Bâkiye(“Geride kalan yüzyıllar”)”’yi tamamlayıp,Sultan Kâ-bus’a sundu.Bu yapıtında Âdem’den Nuh Tufanı’na kadarki olaylar dizisini ta-rihsel,toplumsal,dinsel bakımdan ele almış;Türkler’in,Yunanlılar’ın,Araplar’ın ve İranlılar’ın kullandıkları takvimler konusunda bilgi vermiştir.

1003(Ya da 1009) yılında yeniden Harzem’e dönerek,bilginlere büyük ola-naklar sağlayan Sultan Memun bin el-Memun’un sarayında İbni Sina,İbn Miske-veyh,Ebu Nasr gibi bilginlerle çalıştı.Bu dönemde kendinden on yaş küçük olan İbni Sina ile ısı ve ışık iletimi,maddenin devinimi konularında verimli tartışma-lar yaptı ve yapıtlarında bu tartışmaları açıkladı.Biruni,1017’de Gazneli Mah-mud’un Harezm ülkesini fethetmesinden sonra Gazne kentine yerleşti;gerek Gazneli Mahmud döneminde,gerek Gazneli Mahmud’un oğlu Mesud ve torunu Mevdud dönemlerinde büyük saygınlık görerek ömrünün son yıllarını burada geçirdi.

Biruni’nin hangi ulustan olduğu kesin olarak bilinmiyorsa da şifalı otlar ve bazı ilaçlar konusunda bilgi veren Kitâbu’s-Saydane’nin (“Eczacılık Kitabı”)ön sözüne yazdığı “Ana dilim yetersiz olduğundan,bilim dili olan Arapça ve edebi-yat dili olan Farsça’yı kullandım.” cümlesinden yola çıkılarak,Türk olduğu ileri sürülmüştür.Aynı zamanda bir şair ve düşünür olan bu büyük İslâm bilginin tarih,coğrafya,astronomi,fizik ve kimya dallarında birçok yapıtı vardır.

Nihâyâti’l-Emâkin(“Mekanların sonları”)adlı yapıtı,coğrafyadan,jeoloji ve jeodeziye(Yeryüzü düzlemini ölçme bilgisi)kadar bir dizi konudaki yazıların toplamından oluşmuştur.Sultan Mesud’a sunduğu el-Kanunü’l Mesudi adlı en önemli astronomi yapıtında,Dünya coğrafyası,enlem ve boylam hesapları Dünya çapının ölçümü,Güneş,Ay ve gezgenlerin devinim cetvelleri gibi araştırma ve çalışmalarını toplayan Biruni bilim tarihçilerine göre Kopernik’le başlayan çağ-daş astronominin temellerini atmıştır.Batlamyus ve Aristo’nun kuramlarına kar-şı çıkarak,Dünya’nın durağan değil,dönen bir kütle olduğunu kanıtlamaya çalış-mıştır.

Kitabu’l-Camahir fi Marifeti’l-Cevahir(“Cevherlerin Özellikleri Üstüne”) adlı yapıtında minerallerin ve bazı değerli taşlarının özelliklerini tanıtmış,23 katı ve 6 sıvı maddenin özgül ağırlıklarını bugünkü değerlerine çok yakın olarak sap-tamıştır.Kimi araştırmacılara göre 113,kimi araştırmacılara göre de 180 yapıtı olduğu ileri sürülen Biruni ‘nin ancak 27 yapıtı günümüze kalabilmiştir.Bilim ve felsefe alanındaki çalışma ve araştırmalarında büyük ölçüde İslam düşüncesinin etkisi altında kalmış olan Biruni,evrenin “Öncesiz” olmadığını,bir Tanrı’nın var-lığına gereksinimi olduğunu ileri sürmüştür.Biruni bu savı ile,evrenin “Öncesiz” olduğu düşüncesini savunan İbni Sina’dan ayrılır.Batı’da “Aliboron” adıyla bili-nen Biruni’nin yapıtları birçok Batı diline çevrilmiştir.

Sınav Stresini Azaltan Yiyecekler

“Sınava çok az var, yemek yiyeceğime ders çalışayım”, “Şu testi bitireyim, hamburger siparişi verelim”, “Anne konu çalışıyorum, şimdi su içmenin zamanı mı?” Bunlar üniversite sınavına girecek öğrencilerden sıkça duymaya alışık olduğumuz ifadeler. Oysaki sağlıklı beslenme LYS sınavına sayılı günler kala başarıyı etkileyebilecek en önemli faktörlerden biri olarak karşımıza çıkıyor.

Bu dönemde sağlıksız beslenme (Aşırı kafein alma, fast food ağırlıklı diyet, fazla asitli içecek tüketimi) sınav stresini artırıp kötü sonuçlara neden olabiliyor. Memorial Ataşehir Hastanesi Beslenme ve Diyet Bölümü’nden Dyt. Şefika Aydın Selçuk, sınav sırasında iyi bir performans sağlamada beslenmenin önemi hakkında şu bilgileri veriyor:

Mayonez ve tavuk gibi çabuk bozulabilecek gıdalardan uzak durun
Sınava girecek kişiler için sınav öncesi beslenmesi ve sınav günü beslenmesi büyük önem taşır. Bu dönemde stres yüksek olduğu için yemek konusunda kişiler zorlanmamalıdır. Herkesin yemek alışkanlığı ve damak zevki farklı olduğundan yararlı diye bazı besinleri yemesi konusunda üzerine gidilmemeli, beslenme alışkanlıklarının dışına çıkılmamalıdır.

Kişinin alışkanlığı olan daha önce yediğinde vücutta reaksiyon vermeyen besinler alınmalıdır. Besin zehirlenmeleri riski olduğu için bir gün öncesinde dışarıda yemek yenmemelidir. Yenilmesi zorunlu ise mayonez, tavuk gibi çabuk bozulabilecek gıdalardan sakınılmalı ve açıkta satılan gıdalar tüketilmemelidir.

Gaz yapacak gıdalar ve ağır yiyeceklerden kaçının
Sınavdan bir gün öncesinde gaz problemi oluşturacak kurubaklagil, lahana gibi besinlerden uzak durulmalıdır. Başarıyı olumsuz etkileyeceği için kızartma, birçok besinin bir araya gelmesiyle oluşan karışık yemekler, çok yağlı, ağır soslu yemekler tercih edilmemeli mümkün olduğu kadar hafif, yağsız besinler tüketilmelidir.

Çay kahve tüketimini azaltın
Özellikle bu dönemde çok fazla çay, kahve ve kola içmek kalp çarpıntısına, huzursuzluğa, geç saatlerde de uykusuzluğa, korku ve endişeye neden olur. Kolalı içeceklerde bol miktarda kafein içerir. Bunların yerine C vitamini içeriği yüksek kuşburnu, papatya, adaçayı gibi bitki çayları tüketmek daha doğrudur.

Stresinizi doğru bir yaşam planı ile yenin

Güne kahvaltısız başlamayın
Gün içinde 5-6 öğün yiyecek tüketin (2-3 saatte bir beslenmeye gayret edin)
Kafein içeren içecek ve yiyeceklerden mümkün olduğu kadar uzak durmaya çalışın (Asitli içecekler, kahve, aşırı miktarda çikolata vb)
Aşırı tuz (salamura yiyecekler) ve şeker içeren gıdaları dikkatli tüketmeye çalışın
Gaz yapıcı özelliği olan yiyeceklere dikkat edin (kurubaklagiller asitli içecekler vb)
İçeriğini bilmediğiniz yiyecek-içeceklerden uzak durun ve mümkün olduğunca dışarıdan yemek yememeye gayret edin
Açık havada hoşlandığınız spor ve aktiviteleri yapın

C vitamini yönünden zengin beslenin
Stres anında bıkkınlık ve isteksizlik artar. Uykuya eğilim azalır. Dolayısıyla sınav öncesi düzenli uyumak ve uyku alınmış şekilde sınava girmek çok önemlidir. Stresi azaltmada C vitamininden zengin beslenmenin adrenalin seviyesini artırdığı ve stresi azalttığı gözlenmiştir. Bu sebeple C vitaminden zengin meyve ve sebzeler sıkça tüketilmelidir. Örneğin portakal, kivi, patates, biber, havuç, brokoli gibi sebze ve meyveler C vitaminince zengindir. Özellikle balık, ceviz, zeytinyağı, yeşil yapraklı sebzeler, kırmızı et, pekmez, maydanoz, yeşilbiber, kivi, portakal, kuşburnu mutlaka haftalık ve günlük beslenmenizde yer vermeye çalışın.

İdeal bir sınav sabahı kahvaltısı yapın
Sabah stresle beraber mide bulantısı ve iştahsızlık olması çok doğaldır. Bu yüzden diğer zamanlara göre daha az besin tüketmek istenebilir. Miktarlar az tutularak sağlıklı besinlerin tüketimi sağlanmalıdır. Çok fazla miktarda ve karışık yağlı besinlerin tüketimi de sabah önerilmez.

Örnek kahvaltı menüsü:

1 bardak meyve suyu (Taze sıkılmış tercih edilir)
1-2 dilim peynir
1 yumurta (Haşlanmış veya yağsız tavda omlet)
3 tam ceviz veya 5-6 badem
4-5 adet zeytin
1tatlı kaşığı pekmez
2 -3 dilim tam buğday ekmeği
1kivi veya 5-6 çilek veya 1 yemek kaşığı kuru üzüm
Domates, salatalık

Beynim daha iyi çalışsın diye şeker tüketmek yapılan en büyük hata
Yapılan en büyük hata beynin şeker ile çalışmasından dolayı fazla miktarda çikolata ve basit şeker içeren tatlıların tüketimidir. Fazla şeker tüketimi daha hızlı şekeri düşürecektir. Kan şekeri hızla düşen kişilerde konsantrasyon azalır, el ve ayaklarda uyuşma artar hipoglisemi gözlenir. Bu açıdan tek başına şekerli şeyler değil, kaliteli proteinlerden oluşan bir örüntü de kahvaltı esastır.

Stresi azaltan ve mutluluk veren (seratonin salgılayan) besinler

Tam buğday ekmeği, bulgur pilavı, makarna, tam buğday unundan yapılmış kekler vb.
Peynir, süt ve yumurta
Muz, kivi çilek
Yeterli miktarda çikolata (fazla tüketimi B vitamin depolarını azaltır konsantrasyonu da düşürür)

İsimleriyle iştah kapatan, lezzetleriyle uçuran 10 yemek

İlk kez isimleri duyulduğunda burun kıvırtan, yanlışlıkla tadına bakıldığında hayran bırakan yemekleri derledik. Sevenlerine afiyet olsun.

Kuskus.

Tükürük köftesi.

Kerhane tatlısı.

Mumbar dolması.

Tırnaklı pide.

Kelle paça.

Beyin salatası.

Dil söğüş.

İşkembe çorbası.

Sakallı.

Migren İçin Beslenme Önerileri

Migren hastalığı bir çok insanın ortak problemidir ve çok yaygın bir şekilde görülür. Özellikle yorgunluk ve stresin tetiklediği migrenin bir çok farklı nedeni olabilir. Nörolojik nedenler, cinsel nedenler ve alerjik nedenler migreni tetikleyebilir.

Migren ağrıları için bitkisel tedavi yöntemleri olduğu gibi beslenme de migren için çok büyük önem taşıyor. Yediklerinize dikkat etmeniz hem migren ağrılarından ve migren ataklarından kurtulmanız hemde migren tedavisinde çok önemli bir aşama katetmenizi sağlıyor. Peki migren hastaları neleri yemeli ve neleri yememeli? Hangi besinler migreni tetikliyor, hangi besinler migrene iyi geliyor? İşte merak ettiğiniz bütün soruların cevapları;

Ara Öğünler

Evet: Havuç, kereviz, kahverengi şeker, vanilyalı gofret, şekerli kurabiyeler, yulaflı kurabiyeler, pirinçli vanilyalı pudingler (sütlaç gibi), vanilyalı dondurma.

Hayır: Patates cipsi, fındık, ceviz, krakerler, zeytin, çikolatalı şekerlemeler, salamura balıklar, fıstık ezmeli kurabiyeler, poğaça, çikolatalı puding, çikolatalı dondurma.

İçecekler Listesi

Evet: Kolasız, alkolsüz içecekler, elma suyu, bitki çayları, bir portakaldan hazırlanmış portakal suyu.

Hayır: Kolalı içecekler, günde iki fincandan fazla kahve, bira, viski, cin, brendi, şeri, kırmızı şarap.

Süt ve Süt Ürünleri

İzin verilen:  Az yağlı, kaymağı alınmış süt, diyet süt.

Kısıtlanacak:  Yoğurt, çeyrek ila yarım kaplık porsiyonlar halinde alınmalıdır. Kısıtlanacak diğer besinler ise beyaz peynir ve krem peynirdir.

Kaçınılacak:  Çikolatalı süt, ayran, ekşimik peynir (gravyer, rokfor, çedar vb.)       ekşi elma.

Et, Balık, Kümes Hayvanları

İzin verilen :  Taze sığır, dana, kuzu eti, taze balık veya su içinde konservelenmiş balık.

Kısıtlanacak : Yağ ve tuz içinde konservelenmiş balık.

Kaçınılacak : Konserve et ve yahniler, tütsülenmiş balık, Salam, sosis ve sucuk çeşitleri, jambon, sardalya, pastırma, et tatlandırıcıları ve yumuşatıcıları, hidrolize bitkisel protein ürünleri (soya sosu gibi.)

Ekmek, Fırın Mamulleri, Tahıllar

İzin verilen :  Bisküviler, pankekler, çikolata, fındık ve ceviz ihtiva etmeyen kurabiyeler, her türlü pişmiş tahıl.

 Kısıtlanacak : Kabartma tozuyla yapılmış kek ve poğaçalar, mayalı ekmekler (tam buğday ekmeği, beyaz ekmek, çavdar ekmeği) üzümlü ekmekler.

 Kaçınılacak : Sıcak mayalı ekmekler ve kahveli kek, ekşi hamurdan ekmek, mayalı  poğaçalar, tuzlu krakerler, peynirler, maya ekstreli tatlandırıcılar,  çikolata, fındık, ceviz ve hindistan cevizli içeren gıdalar.

Meyve ve Sebzeler

İzin verilen :  Aşağıdakilerin dışında hepsi.

Kısıtlanacak : Kuru incir, üzüm, muz (günde en çok yarım adet), ananas, günde en fazla bir adet portakal veya mandalina.

Kaçınılacak  : Papatya, erik, korservelenmiş ve dondurulmuş tuzlu sebzeler, ekşi otlar, paket çorbalar, taze fasulye ve fava fasulyesi (bakla).

Bakliyat, Fındık, Ceviz

İzin verilen    : –  

Kısıtlanacak: –      

Kaçınılacak: Fasulye türleri, bezelye, fıstık ve fındık ezmesi, fındık, ceviz, badem

Diğer Besinler

İzin verilen:  Sirke   

Kısıtlanacak : Salata sosları (1–2 kaşıkla sınırlanacaktır), votka (içmek zorunda iseniz)

Kaçınılacak  : Mono sodyum glutamat (hazır et suyu tabletleri) soya sosu, et  tatlandırıcıları.

Neden Öksürürüz ?

Öksürük nedir? Öksürüğün nedenleri nelerdir? Öksürük nasıl geçer, öksürük tedavisi hakkında bilgi.

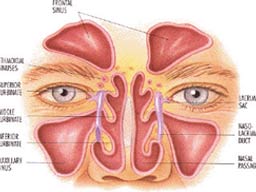
Öksürük çoğu kimse tarafından önemsenmeyen, aslında önemli hastalıkların habercisi olan bir rahatsızlıktır. Öksürük genelde, vücudun yabancı bir maddeye, kan toplanmasına, ciğerlerde ya da boğazda soğuk algınlığı, sigara veya alerji nedeniyle oluşan bu tahrişe karşı doğal bir tepkisidir. Balgamlı ve kuru olduğu durumlar vardır.

Bir haftadır süren öksürüğünüz 38 derece ve yukarısında ateş yapıyorsa ve soluk alma güçlüğü de çekiyorsanız, zatürre olasılığı akla gelmelidir. Zatürre özellikle yaşlılarda ve sağlıksız kimselerde tehlikeli olan akciğer iltihaplanmasıdır. Hemen doktora başvurulmalıdır. Doktor, ateşi düşürmek ve rahatsızlığı gidermek için suda eriyen aspirin ya da parasetamol önerebilir. Antibiyotik tedavisi ve ileri durumlarda hastane tedavisi gerekebilir.

Ateşiniz yok, nezleniz yok, soluk almada güçlük çekmiyorsunuz, fakat öksürükten grimsi ya da çoğunlukla yeşilimsi bir balgam geliyorsa, kronik bronşit olasılığı vardır. Solunum yollarınızda sürekli bir iltihaplanma olmuştur. Doktora başvurun, antibiyotik tedavisi uygulayabilir.

Ateş, nezle, soluk almada güçlük ve balgam çıkarma olmadığı halde, birkaç haftadır giderek kötüleşen bir öksürükle karşı karşıya iseniz, tüberkülozdan ya da akciğer kanserinden kuşkulanmak gerekir. Hemen doktora
koşun.

Uzun zaman süren kuru öksürükler, bir alerji ya da sigara nedeniyle nefes borusunda iltihaplanmadan da ileri gelebilir. Sigara genelde olduğu gibi, özellikle göğüs sağlığı açısından çok zararlıdır. Yukarıda sayılan öksürük türlerinin her birinde kesinlikle sigara içilmemelidir.

TERMOS NASIL SICAĞI SICAK, SOĞUĞU SOĞUK TUTUYOR?

TEK NEDENİ VARDIR, VAKUM.YANİ BOŞLUK.BİR TERMOSTA İÇİÇE GEÇMİŞ İKİ KAP VARDIR.DIŞTAKİ METAL BİR KAP OLUP İÇTEKİ GENELLİKLE BİR CAM ŞİŞEDİR.İKİSİNİN ARASINDAKİ HAVA İSE BOŞALTILMIŞTIR.TAM OLMASA DA ÜRETİCİLER TARAFINDAN ELDE EDİLEBİLEN TAMA YAKIN BİR BOŞLUK VARDIR.VAKUMLU BİR ORTAMDA HAVA MOLEKÜLLERİ DE ILMADIĞINDAN ISI İLETİLEMEZ.CİSMİN ISISI BAŞLANGIÇTA NE İSE O HALDE KALIR.İÇERDEN DIŞARIYA, DIŞARDAN İÇERİYE ISI GEÇİŞİ OLMAZ.

ATEŞ BÖCEĞİ NASIL IŞIK SAÇIYOR?

ASLINDA BU BÖCEĞİN VERDİĞİ IŞIĞIN ATEŞLE DE SICAKLIKLA DA BİR İLGİSİ YOKTUR. BİLİMSEL ADI "SOĞUK IŞIK"TIR. BU IŞIK OLAYI, MOLEKÜLER SEVİYEDE KİMYASAL BİR İŞLEMDİR. BAZI MOLEKÜLLERİN AYRIŞARAK DAHA YÜKSEK ENERJİLİ HALE GEÇEBİLDİKLERİ VE BU FAZLA ENERJİYİ IŞIĞA DÖNÜŞTÜREBİLDİKLERİDİR. ATEŞ BÖCEĞİNİN KARIN BÖLGESİNDEKİ IŞIK ORGANINDA BULUNAN GUDDELERDEN IŞIK ELDE ETMEDE ROL ALAN İKİ ANA KİMYASAL MADDE ÜRETİLMEKTEDİR.

KUŞLAR NASIL KONUŞABİLİYOR?

HER İNSAN AĞZIYLA KONUŞUR AMA KONUŞABİLMEYİ SAĞLAYAN ASIL ORGAN BEYİNDİR. BEYİNDE OLUŞAN DÜŞÜNCELER DİLİMİZE VE DUDAKLARIMIZA AKTARILIR. HAYVANLAR BU NEDENLE KONUŞAMAZ. PAPAĞAN VE BENZERİ KUŞLARIN YAPTIKLARI KONUŞMA DEĞİL, MÜKEMMEL BİR SES TINISI EZBERİ VE TEKRARDIR. SESLERİ EZBERLER VE TAKLİT EDERLER. KUŞLARIN SES ORGANLARI MEMELİ HAYVANLARDAN FARKLI OLARAK GIRTLAKTA DEĞİL GÖĞÜS KAFESLERİNN DİBİNDE, KARIN BOŞLUĞUNUN DERİNLİKLERİNDEDİR.

ÜÇ YAŞINDAN DAHA ÖNCE OLANLARI NİÇİN HATIRLAMIYORUZ?

BİLİM ADAMLARI GEÇMİŞ DENEYİMLERİMİZİ SAKLAYAN HAFIZAMIZIN BEYNİMİZDE ANIVEYA ÖYKÜ ŞEKLİNDE ORGANİZE OLDUĞUNU İLERİ SÜRÜYORLAR. ÜÇ YAŞINDAN KÜÇÜKLER BU ŞEKİLDE İLETİŞİM KURMA YETENEĞİNE SAHİP DEĞİLLER.ÖYKÜ VE ANILARINI ANLATAMIYORLAR. YER VE KARAKTER KAVRAMLARINI ANLAMIYORLAR. ÜÇ YAŞINDAN KÜÇÜKLER DÜZGÜN KONUŞABİLDİKLERİ,ANLAYIŞ, SEZİŞ VE HAFIZA YETENEKLERİNE SAHİP OLDUKLARI HALDE TÜM OLANLARI BİR BÜTÜN OLARAK ŞEKİLLENDİREMİYOR.

DOLUNAY İNSAN DAVRANIŞLARINI ETKİLER Mİ?

İNSANLAR ARASINDA BU İNANÇ OLDUKÇA YAYGINDIR. ESKİLERİN AY'IN DÖNEMLERİNE BAĞLADIKLARI BOŞ BİR İNANCIN GÜNÜMÜZE UZANAN BİR VARSAYIMIDIR. BİLİM ADAMLARININ YAPTIKLARI BÜTÜN ÇALIŞMALAR BU GÖRÜŞÜN BOŞ OLDUĞUNU KANITLAMIŞTIR. AY, DÜNYADAKİ OKYANUSLARIN GEL-GİT DENİLEN SULARIN ALÇALMASI VE YÜKSELMESİ OLAYI ÜZERİNDE DOĞRUDAN ETKİSİ VARDIR. VÜCUDUMUZDAKİ SUYUN ORANI , OKYANUSLARDAKİ SU MİKTARIYLA KIYASLANAMAZ.

İNSAN KORKUNCA NİÇİN DİŞLERİ BİRBİRİNE VURUR?

BİR İNSAN BÜYÜK BİR TEHLİKE VEYA KORKU VERİCİ OLAYLA KARŞILAŞINCA VÜCUDU OTOMATİKMAN SAVUNMAYA GEÇER. DİĞER CANLILARDA OLDUĞU GİBİ DİŞLER VE ÇENE SAVUNMANIN ANA MEKANİZMALARIDIR.İŞTE BU NEDENLE İLK İNSANLARDAN GELEN KALITIMSAL YAPIDAN DOLAYI ÖNCE ÇENE VE DİŞLER HAREKETE GEÇER. ÇENEDEKİ KASLAR TİTRER, BU DA SANKİ DİŞLER BİRBİRİNE VURUYORMUŞ GİBİ GÖRÜNTÜ VERİR.

BİR HAFTA NİÇİN 7 GÜNDÜR?

BABİLLİLER 7 GÜNLÜK HAFTAYI ZAMAN BİRİMİ OLARAK KULLANIYORLARDI. İLK ÇAĞLARDA BİLİNEN BEŞ GEZEGEN İLE GÜNEŞ VE AYIN SAYISI NIN 7 OLUŞU BU SAYIYI GİZEMLİ VE UĞURLU KILIYORDU. DAHA SONRA DİNLERDE GÖĞÜN 7 KAT OLUŞU VE DOĞADAKİ ANA RENK SAYISININ 7 OLUŞU, MÜZİK NOTALARININ 7 OLUŞU SAYININ ÖNEMİNİ DAHA ÇOK BELİRTTİ. DAHA SONRA FRANSA TAKVİM YAPISINI DEĞİŞTİREREK HAFTA SAYISINI 10 YAPTI AMA KABUL GÖRMEDİ. RUSYA 5 GÜNLÜK HAFTA UYGULAMASINA GEÇTİ, O DA TUTULMADI.

İNSANLAR SAATLERİNİ NİÇİN SOL KOLLARINA TAKARLAR ?

ÖZEL BİR DURUM VEYA FARKLI OLMA DÜŞÜNCESİ YOKSA İNSANLARIN ÇOĞU SAATLERİNİ SOL KOLA TAKAR. ÇÜNKÜ ÇOĞUNLUK SAĞ ELİNİ KULLANMAKTADIR VE BU KOLUN DAHA HAREKETLİ OLMASI NEDENİYLE SAATİN BİR YERLERE ÇARPIP ZARAR GÖRME OLASILIĞI YÜKSEKTİR. ZATEN SAATİN KURMA DÜĞMESİ 3 RAKAMININ YANINDADIR. İNSANLAR SAATİ KURMAK İSTEDİKLERİ ZAMAN ONU BİLEKTEN ÇIKARMADAN SAĞ ELLE UZATTIKLARI SOL KOLLARINDAKİ SAATİ KURABİLİRLER.